Visualizing geometric product relationships in plane geometry

07 Jan 2019

In previous posts, I have shown how to visualize both the dot product and the wedge product of two vectors as parallelogram areas. In this post, I will show how the dot product and the wedge product are related through a third algebraic product: the geometric product. Along the way, we will see that the geometric product provides a simple way to algebraically model all of the major geometric relationships between vectors: rotations, reflections, and projections.

Before introducing the geometric product, let’s review the wedge and dot products and their interpretation in terms of parallelogram areas.

Given two vectors, a and b, their wedge product, a \wedge b, is straightforwardly visualized as the area of the parallelogram spanned by these vectors:

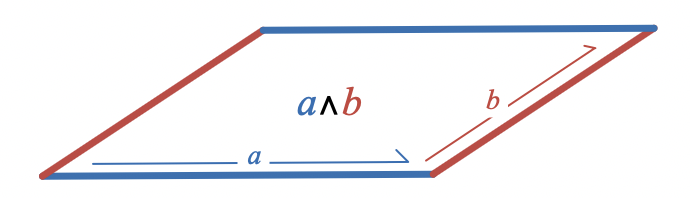
Recall that algebraically, the wedge product a \wedge b produces an object called a bivector that represents the size and direction (but not the shape or location) of a plane segment in a similar way that a vector represents the size and direction (but not the location) of a line segment.

The dot product of the same two vectors, a \cdot b, can be visualized as a parallelogram formed by one of the vectors and a copy of the other that has been rotated by 90 degrees:

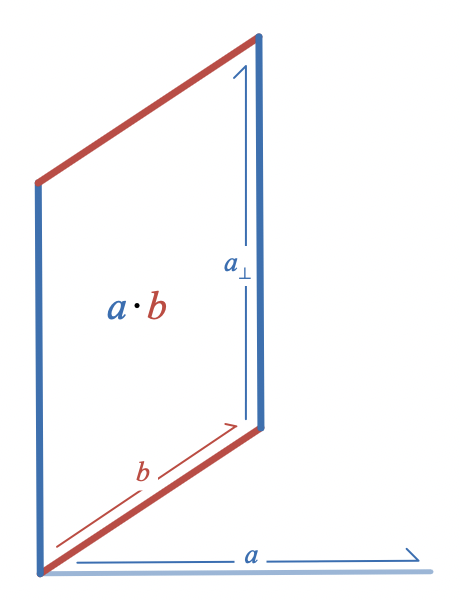
Well, almost. When I originally wrote about this area interpretation of the dot product, I didn’t want to get into a discussion of bivectors, but once you have the concept of bivector as directed plane segment, it’s best to say that what this parallelogram depicts is not quite the dot product, a \cdot b, which is a scalar (real number), but rather the bivector (a \cdot b) I where I is a unit bivector.

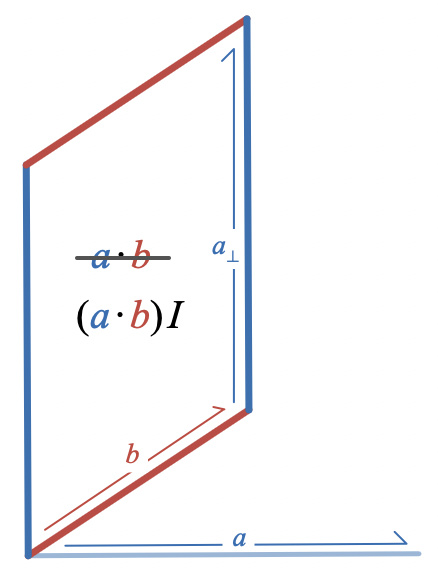
Dot product of vectors a and b as a parallelogram should include a factor of I

The scalar a \cdot b scales the unit bivector I to produce a bivector with magnitude/area a \cdot b. It’s hard to draw a scalar on a piece of paper without some version of this trick. Once you’re looking for it, you’ll see that graphical depictions of real numbers/scalars almost always show how they scale some reference object. It could be a unit segment of an axis or a scale bar; here it is instead a unit area I.

Examining the way that the dot product and the wedge product can be represented by parallelograms suggests an algebraic relationship between them:

(a \cdot b) I = b \wedge a_\perp

where a_\perp represents the result of rotating a by 90 degrees. Since the dot product is symmetric, we also have

(a \cdot b) I = a \wedge b_\perp

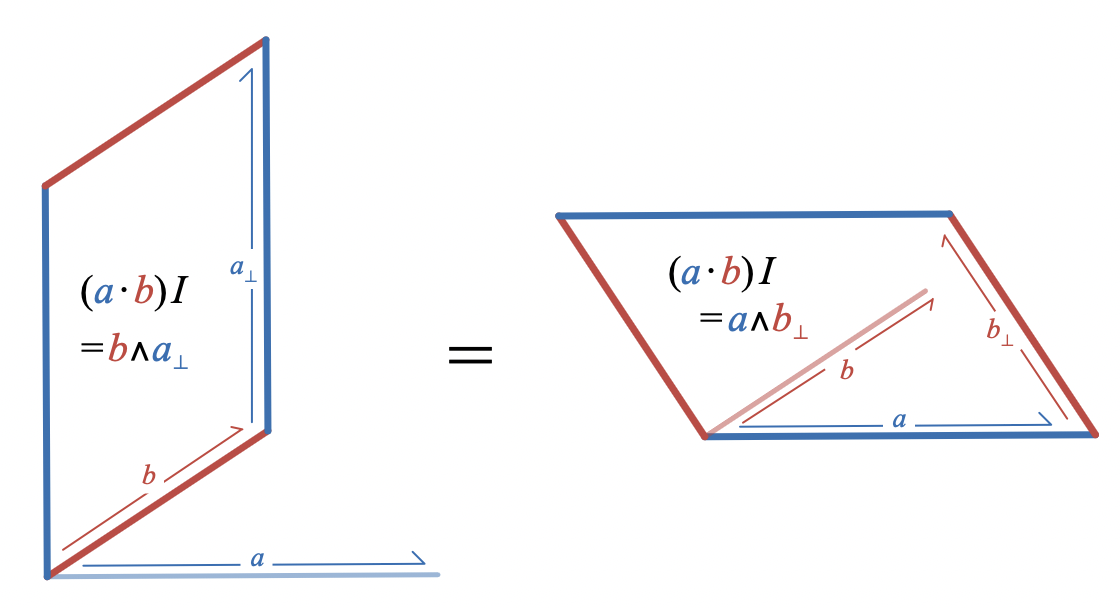
Relationship between dot and wedge product

To really understand this relationship, we’ll need an algebraic way to represent how a_\perp is related to a; in other words, we’ll need to figure out how to represent rotations algebraically.

To work towards an algebraic representation of rotations, recall how the dot product and wedge product can be expressed in terms of lengths and angles:

\begin{aligned} a \cdot b &= |a| |b| \cos(\theta_{ab}) \\ a \wedge b &= |a| |b| \sin(\theta_{ab}) I \end{aligned}

If you’re familiar with complex numbers, then adding these two products together produces a very suggestive result:

\begin{aligned} a \cdot b + a \wedge b &= |a| |b| (\cos(\theta_{ab}) + \sin(\theta_{ab}) I) \\ &= |a| |b| \exp(\theta_{ab} I) \end{aligned}

where the second line is an expression of Euler’s Formula^⊕At this point, it probably isn’t so clear what it could mean to exponentiate a bivector. Suspend disbelief, I’ll come back to this..

In words, the sum of the dot product and the wedge product of two vectors is the product of their lengths, |a| and |b|, and a factor representing the rotation between their directions, \exp(\theta_{ab} I). This sum is so geometrically meaningful that Geometric Algebra gives it its own name: the geometric product, and its own notation, simple juxtaposition of vectors:

a b = a \cdot b + a \wedge b = |a||b| \exp(\theta_{ab} I)

Since the dot product is symmetric, but the wedge product is anti-symmetric, the order of the factors in a geometric product matters. The reverse of this product is

\begin{aligned} b a &= b \cdot a + b \wedge a \\ &= a \cdot b - a \wedge b = |a||b| \exp(-\theta_{ab} I) \end{aligned}

These product formulas can be solved in order to represent the dot product and wedge product in terms of the geometric product^⊕As an alternative, it is possible to define the geometric product as a linear, associative product between vectors such that the square of a vector is a scalar, and then define the dot product and wedge product as the symmetric and anti-symmetric parts of the geometric product.,

\begin{aligned} a \cdot b &= \frac12(ab + ba) \\ a \wedge b &= \frac12(ab - ba) \end{aligned}

In other words, the dot and wedge products are half the symmetric and anti-symmetric sums of the geometric product and its reverse.

Using these relations gives a very interesting way to characterize parallel and perpendicular vectors: vectors are parallel when their wedge product is zero, so that the geometric product commutes:

a \parallel b \Leftrightarrow a \wedge b = 0 \Leftrightarrow a b = b a

and they are perpendicular when their dot product is zero, so that the geometric product anti-commutes:

a \perp b \Leftrightarrow a \cdot b = 0 \Leftrightarrow a b = - b a

In general, for vectors that are neither perpendicular nor parallel, the geometric product is neither commutative nor anti-commutative. For this reason, it’s important to keep track of the order of terms in a multiplication when using the geometric product. We’ll see that with the geometric product, you can get an awful lot of geometry done by thinking about when the order of various symbols can be swapped.

Properties of the geometric product

Vectors square to scalars

Since the wedge product of a vector with itself is always 0, the geometric product of a vector with itself is equal to the dot product of that vector with itself:

a a = a^2 = a \cdot a = |a|^2

Associative

The geometric product has another property that is less obvious from its decomposition as the sum of the dot and wedge products: it is associative,

(a b) c = a (b c) = a b c

Associativity is extremely useful algebraically. Combined with the fact that vectors square to real numbers (scalars), associativity means that equations involving products of vectors can be solved. For example, given

a b = c d

if we know b, we can solve for a by first multiplying on the right by b

\begin{aligned} a b b &= c d b \\ a b^2 &= c d b \\ a |b|^2 &= c d b \end{aligned}

and then dividing through by the scalar |b|^2

a = c d \frac{b}{|b|^2}

Invertible

Another way to say that we can solve equations involving geometric products is to say that under the geometric product, vectors have unique inverses. This is a consequence of associativity and the fact that vectors square to scalars.

For an inverse of vector b, we require

b b^{-1} = 1

Multiplying both sides of this equation by b gives

b^2 b^{-1} = b

and dividing by the scalar b^2 = |b|^2 gives a formula for the inverse of a vector:

b^{-1} = \frac{b}{b^2} = \frac{b}{|b|^2}

In other words, to find the inverse of a vector, divide the vector by the square of its length.

Since the order of geometric multiplications matters in general, we should check that b^{-1} b also equals 1:

b^{-1} b = \frac{b}{b^2} b = \frac{b^2}{b^2} = 1

Neither the wedge product nor the dot product alone admit unique inverses, but their sum, the geometric product, contains just the right information to admit a unique inverse.

Interpreting the geometric product geometrically

Algebraically, the geometric product has some very useful properties, but how can we interpret it geometrically?

To simplify, let’s first consider the geometric product of two unit vectors. I’ll use the notation \hat{a} to represent the unit vector in the same direction as a:

\hat{a} = \frac{a}{|a|}

so that

|\hat{a}| = \frac{|a|}{|a|} = 1

and

\hat{a}^2 = |\hat{a}|^2 = 1

We will use the fact that the square of a unit vector is 1 in the process of simplifying several expressions below.

Recalling the lengths-and-angles formula for the geometric product,

a b = |a| |b| (\cos(\theta_{ab}) + \sin(\theta_{ab}) I) = |a| |b| \exp(\theta_{ab} I)

we can see that the geometric product of two unit vectors effectively represents the rotation between them:

\hat{a} \hat{b} = \cos(\theta_{ab}) + \sin(\theta_{ab}) I = \exp(\theta_{ab} I)

The rotation represented by \hat{a}\hat{b} can be applied to another vector in the plane, v, by multiplying on the right (remember, order matters) to form v\hat{a}\hat{b}^⊕Some care is required for rotations in more than two dimensions. When v is not in the same plane as a and b, then v\hat{a}\hat{b} no longer represents a rotation of v. A closely related formula does generalize: \hat{b}\hat{a}v\hat{a}\hat{b} is a rotation of v by twice the angle between a and b in any number of dimensions even when v, a, and b are not all in the same plane.:

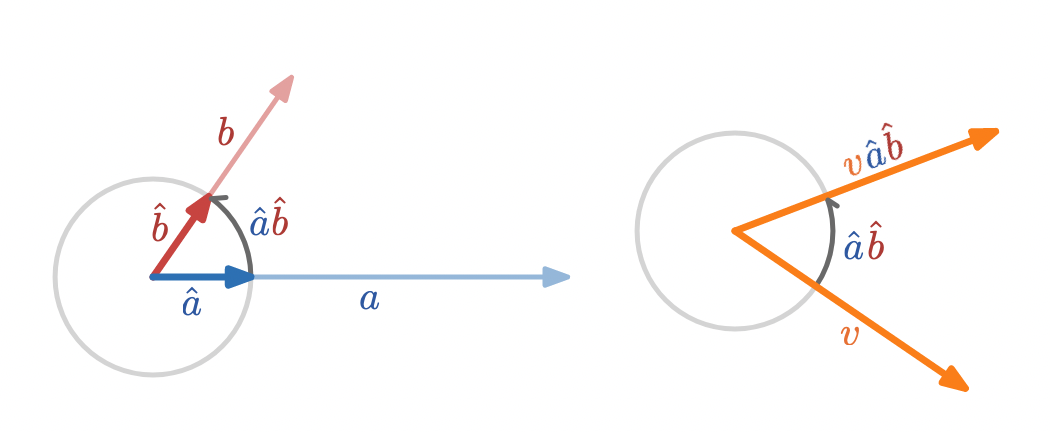
As a check,

\hat{a} (\hat{a} \hat{b}) = (\hat{a} \hat{a}) \hat{b} = \hat{b}

so right multiplication by \hat{a}\hat{b} rotates \hat{a} to \hat{b}.

Reversing the order of factors in a geometric product of unit vectors reverses the sense of rotation, so that \hat{b}\hat{a} is a rotation in the opposite direction as \hat{a}\hat{b}. As a check,

\hat{b} (\hat{b} \hat{a}) = (\hat{b}\hat{b}) \hat{a} = \hat{a}

To compose two rotations represented as geometric products, \hat{a} \hat{b} and \hat{b} \hat{c}, we simply multiply them:

\begin{aligned} (\hat{a} \hat{b}) (\hat{b} \hat{c}) &= \hat{a} \hat{b} \hat{b} \hat{c} \\ &= \hat{a} (\hat{b} \hat {b}) \hat{c} \\ &= \hat{a} \hat{c} \end{aligned}

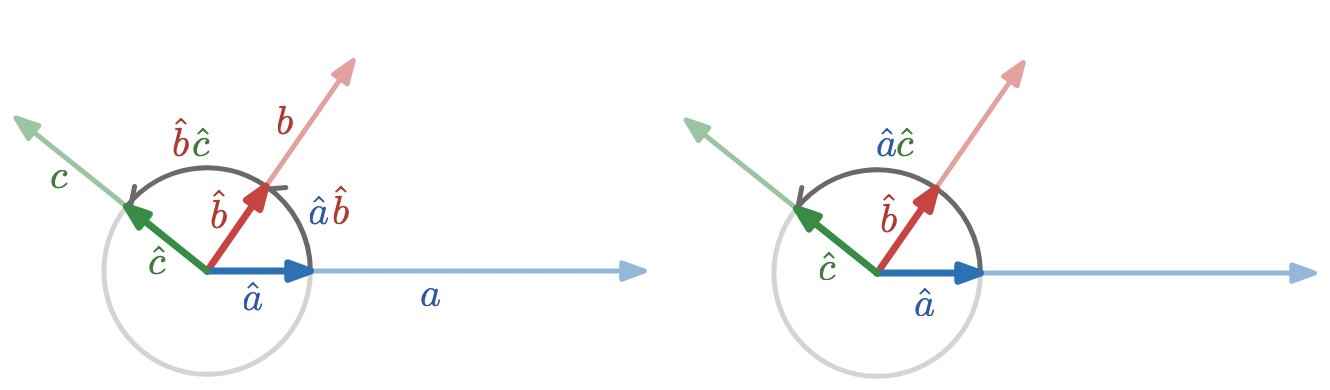
In terms of angles, this represents the same calculation as

\begin{aligned} \exp(\theta_{ab} I) \exp(\theta_{bc} I) &= \exp((\theta_{ab}+\theta_{bc}) I) \\ &= \exp(\theta_{ac} I) \end{aligned}

Triangle angle sum laws

This is enough to start to give geometric product interpretations to some familiar facts about triangles. Given a triangle with edge vectors a, b, and c,

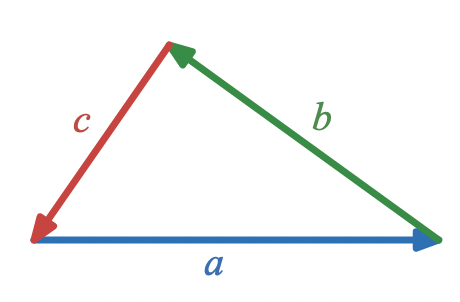
the rotations through the exterior angles are represented by \hat{a}\hat{b}, \hat{b}\hat{c}, and \hat{c}\hat{a}.

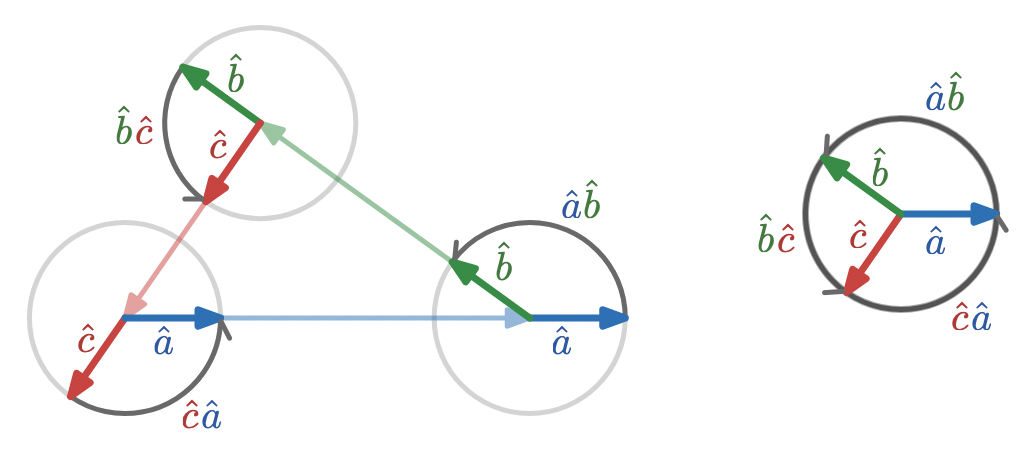
Composition of exterior angles is an identity angle

The composition of exterior angles is a full rotation, which is simply an identity operation for vectors.

To show this algebraically, we simply multiply the geometric products representing each rotation to compose the rotations, and then re-associate:

\begin{aligned} &(\hat{a} \hat{b})(\hat{b} \hat{c})(\hat{c} \hat{a}) \\ &= \hat{a} (\hat{b} \hat{b}) (\hat{c} \hat{c}) \hat{a} \\ &= \hat{a} \hat{a} \\ &= 1 \end{aligned}

A “straight angle”, i.e. a rotation by 180 degrees, is the rotation between \hat{a} and -\hat{a}, which is simply

\hat{a} (- \hat{a}) = -\hat{a}\hat{a} = -1

If the exterior angle rotations of a triangle are \hat{a}\hat{b}, \hat{b}\hat{c}, and \hat{c}\hat{a}, then the interior angle rotations are simply the negatives of each of these, -\hat{a}\hat{b}, -\hat{b}\hat{c}, and -\hat{c}\hat{a}, and so the composition of the interior angles is^⊕One way to visually see that these angles add up to a half-turn is to notice that every sector of the circle has an equal missing sector on the opposite side.

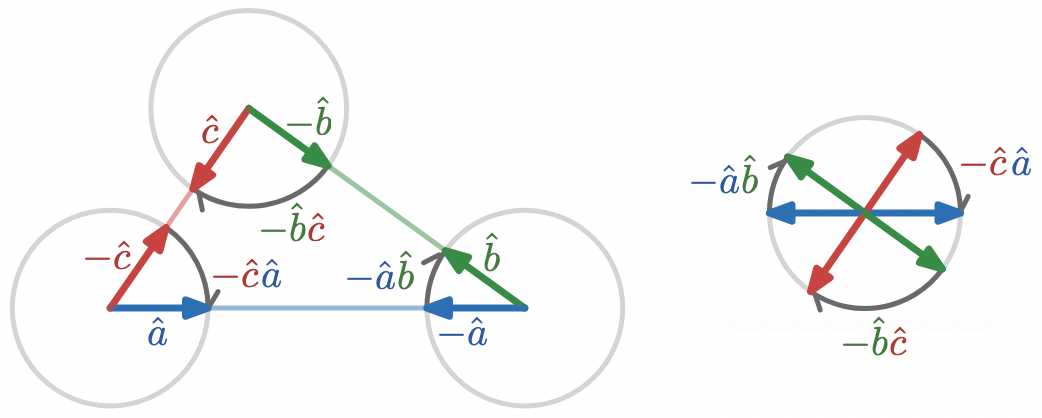
Composition of interior angles is a straight angle

\begin{aligned} &(-\hat{a} \hat{b})(-\hat{b} \hat{c})(-\hat{c} \hat{a}) \\ &= - \hat{a} \hat{b} \hat{b} \hat{c} \hat{c} \hat{a} \\ &= -1 \end{aligned}

which is a straight angle. In other words, the composition of the interior angles of a triangle is a straight angle, i.e. a 180 degree angle.

Right angles

If two unit vectors have zero dot product, so that they anti-commute under the geometric product,

\begin{aligned} \hat{a} \cdot \hat{b} &= 0 \\ \frac12 (\hat{a} \hat{b} + \hat{b} \hat{a}) &= 0 \\ \hat{a} \hat{b} &= -\hat{b}\hat{a} \end{aligned}

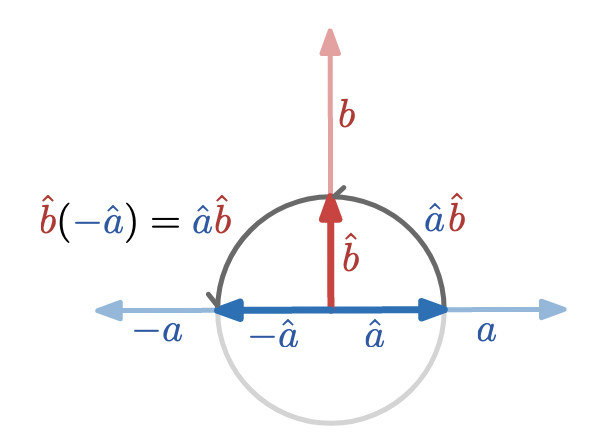
then multiplying both sides on the right by \hat{a}\hat{b} gives

(\hat{a} \hat{b})^2 = -\hat{b}\hat{a} \hat{a} \hat{b} = -1

which we can interpret geometrically as saying that the composition of a right angle with itself is a straight angle. The above manipulation is an algebraic way of representing the fact that the following statements are all equivalent:

two vectors are perpendicular
two vectors have zero dot product
two vectors anti-commute under the geometric product
the angle between two vectors bisects a straight angle

Dilations

For vectors that are not unit vectors, it’s a little easier to supply a geometric interpretation for the geometric ratio, a^{-1}b^⊕Note that for unit vectors, there is no distinction between ratios and products because a unit vector is its own inverse: \hat{a}^{-1}=\hat{a}., than the geometric product ab. In terms of lengths and angles, the geometric ratio is

a^{-1} b = \frac{|b|}{|a|} \left(\cos(\theta_{ab}) + \sin(\theta_{ab}) I\right) = \frac{|b|}{|a|} \exp(\theta_{ab} I)

This is a composition of the rotation that takes the direction of a to the direction of b with the dilation that takes the length of a to the length of b.^⊕In the Argand diagram picture of complex arithmetic, multiplying by a complex number has exactly this same effect of dilation and scaling. In Visual Complex Analysis, Needham calls this an “amplitwist” for “amplification” and “twist”.

Ratios of vectors in the plane behave in exactly the same way as complex numbers; the Argand diagram effectively models vectors in the plane as complex numbers by forming ratios of every vector with a constant unit vector pointing along the “real axis”.

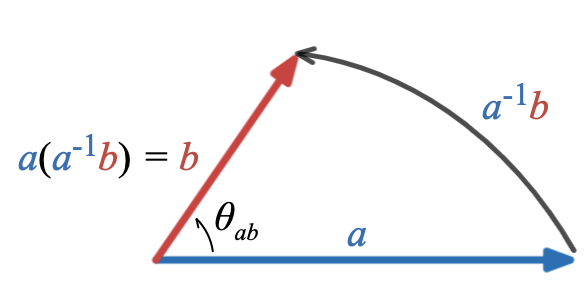
As a check,

a (a^{-1} b) = (a a^{-1}) b = b

Applying the geometric ratio repeatedly produces a sequence of vectors lying on a logarithmic spiral, with adjacent pairs of vectors forming the legs of a sequence of similar triangles.

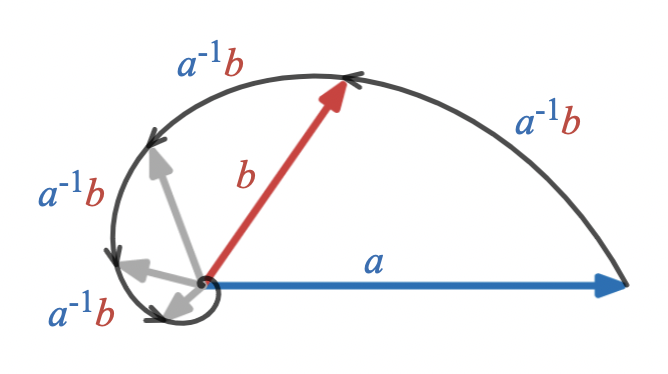
Rotation, Reflection, Projection, Rejection

Reversing the order of the terms in the geometric ratio from a^{-1}b to ba^{-1} reverses the sense of rotation, but leaves the dilation unchanged

b a^{-1} = \frac{|b|}{|a|} \left(\cos(\theta_{ab}) - \sin(\theta_{ab}) I\right) = \frac{|b|}{|a|} \exp(-\theta_{ab} I)

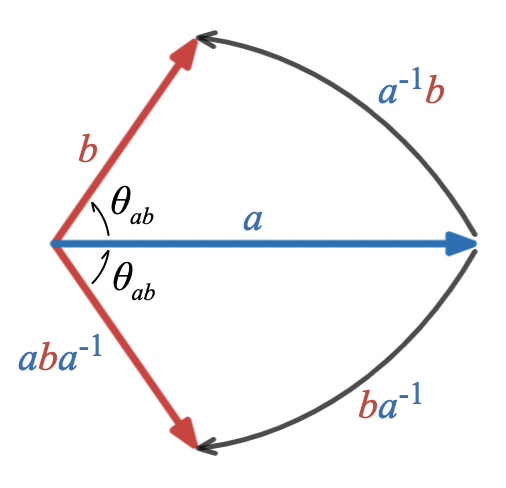
Examining this picture suggests that aba^{-1} is the reflection of b across a. This representation of a reflection is sometimes referred to as a “sandwich product” because b is sandwiched between a and its inverse. It can equivalently be written as \hat{a}b\hat{a} because

\begin{aligned} aba^{-1} &= a b \left(\frac{a}{|a|^2}\right) \\ &= \left(\frac{a}{|a|}\right) b \left(\frac{a}{|a|}\right) \\ &= \hat{a} b \hat{a} \end{aligned}

Notice that aba^{-1} is linear in b, but independent of the scale of a, as expected for a reflection of b across a

This sandwich product expression for reflection makes it particularly evident that a vector and its reflection have the same length. If

b_\mathrm{refl} = a b a^{-1}

then

\begin{aligned} b_\mathrm{refl}^2 &= (a b a^{-1}) (a b a^{-1}) \\ &= a b (a^{-1} a) b a^{-1} \\ &= a b^2 a^{-1} \\ &= b^2 a a^{-1} \\ &= b^2 \end{aligned}

where we have made use of the fact that b^2 is a scalar and so it can be moved freely within a geometric product.

Left multiplying aba^{-1} by the unit factor bb^{-1} gives another representation for the reflection of b across a:

\begin{aligned} aba^{-1} &= (bb^{-1}) (a b a^{-1}) \\ &= b \left(\frac{b}{|b|^2}\right) a b \left(\frac{a}{|a|^2}\right) \\ &= b \frac{b}{|b|}\frac{a}{|a|}\frac{b}{|b|}\frac{a}{|a|} \\ &= b (\hat{b}\hat{a})(\hat{b}\hat{a}) \\ &= b (\hat{b}\hat{a})^2 \end{aligned}

The last line represents applying the rotation between b and a to the vector b twice. In other words, to reflect b across a, rotate b through twice the angle between b and a.

There is a simple relationship between the reflection of b across a and the parallel and perpendicular components (i.e. the projection and “rejection”) of b relative to a: the projection and rejection are the half symmetric and anti-symmetric sums of b and its reflection in a

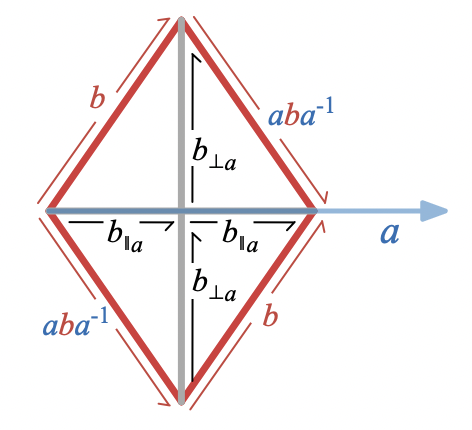
Relationship of reflection, projection, and rejection

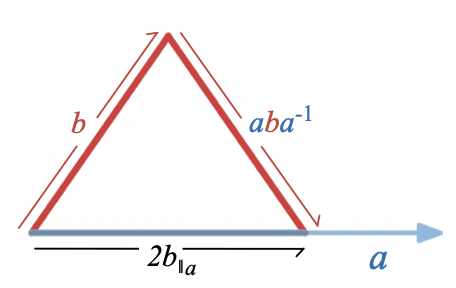
In other words, the sum of b and its reflection across a is twice the projection of b onto a

b_{\parallel a} = \frac12 \left(b + aba^{-1}\right)

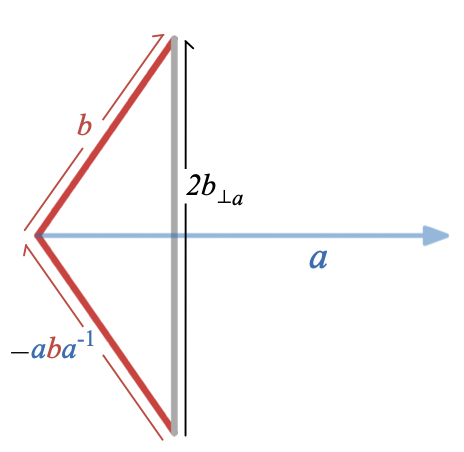
and the difference of b and its reflection across a is twice the rejection of b from a

b_{\perp a} = \frac12 \left(b - aba^{-1}\right)

Using the freedom to insert the unit factor aa^{-1} into the equation for b_\parallel and re-associating gives

\begin{aligned} b_{\parallel a} &= \frac12 \left(b\left(aa^{-1}\right) + aba^{-1}\right) \\ &= \frac12 \left(ba + ab\right)a^{-1} \\ &= (b \cdot a) a^{-1} \\ &= (b \cdot \hat{a}) \hat{a} \end{aligned}

which is a familiar way to interpret the dot product in terms of a projection, and similarly,

\begin{aligned} b_{\perp a} &= \frac12 \left(b\left(aa^{-1}\right) - aba^{-1}\right) \\ &= \frac12 \left(ba - ab\right)a^{-1} \\ &= (b \wedge a) a^{-1} \\ &= (b \wedge \hat{a} ) \hat{a} \end{aligned}

which is a probably less familiar way to interpret the wedge product in terms of rejection.

We can check that combining these components gives back the whole vector b:

\begin{aligned} b &= b(aa^{-1}) \\ &= (ba)a^{-1} \\ &= (b \cdot a + b \wedge a) a^{-1} \\ &= (b \cdot a) a^{-1} + (b \wedge a) a^{-1} \\ &= b_{\parallel a} + b_{\perp a} \end{aligned}

Planarity

We have seen that the condition that three vectors form a triangle is

a + b + c = 0

A similar but weaker condition on three vectors is that they are in the same plane, and the traditional way to state this condition algebraically is in terms of linear dependence:

\alpha a + \beta b + \gamma c = 0

for some set of scalars \alpha, \beta, and \gamma that are not all 0. In words:

A weighted sum of the vectors is 0
It is possible to scale the vectors so that they form a triangle
At least one of the vectors can be written as a weighted sum of the other two

Geometric Algebra provides two ways to restate the planarity condition without the need for introducing extra scalar parameters. Suppose (without loss of generality) that \alpha is non-zero, and wedge on the right by b \wedge c:

\begin{aligned} (\alpha a + \beta b + \gamma c) \wedge (b \wedge c) &= 0 \\ \alpha (a \wedge b \wedge c) + \beta (b \wedge b \wedge c) + \gamma (c \wedge b \wedge c) &= 0 \end{aligned}

The last two terms are 0 by anti-symmetry of the wedge product, and so, after dividing through by the non-zero scalar \alpha, we have

a \wedge b \wedge c = 0

as a restatement of the condition that a, b, and c are in the same plane. A geometrical interpretation of this formula is that the vectors span a parallelepiped with no volume^⊕In general, the wedge product of n vectors is 0 if and only if the vectors all lie in an n-1 dimensional linear subspace. The wedge product of two vectors is 0 when they are directed along the same line, the wedge product of three vectors is 0 when they are in the same plane, and so on..

There is a further alternative statement of the condition of planarity of three vectors using the geometric product that is very useful for proofs in plane geometry. Again starting from

\alpha a + \beta b + \gamma c = 0

and assuming that \alpha is non-zero, multiplying on the right by bc gives

\alpha abc + \beta b^2c + \gamma cbc = 0

and alternatively, multiplying on the left by cb gives

\alpha cba + \beta cb^2 + \gamma cbc = 0

Subtracting this equation from the previous one and noting that b^2c = c b^2 because b^2 is a scalar gives

\alpha (abc - cba) = 0

and dividing by the non-zero scalar \alpha and re-arranging gives

abc = cba

as a third way of stating the condition that three vectors are in the same plane. This condition is harder to extend to other dimensions, but it’s very useful in computations because it means that we’re always free to reverse the geometric product of any three vectors that are in the same plane.

We’ve seen that in order to rotate a vector c by the angle between two other vectors, a and b, we can form

c_\mathrm{rot} = c\hat{a}\hat{b}

and using the planarity condition above to reverse the three vectors shows that multiplying on the right by \hat{a}\hat{b} is equivalent to multiplying on the left by \hat{b}\hat{a}

c_\mathrm{rot} = \hat{b}\hat{a}c

This freedom to reverse triples of vectors in the plane makes it easy to check that rotation preserves length:

\begin{aligned} c_\mathrm{rot}^2 &= (c\hat{a}\hat{b})(c\hat{a}\hat{b}) \\ &= (c\hat{a}\hat{b})(\hat{b}\hat{a}c) \\ &= c\hat{a}\hat{b}^2\hat{a}c \\ &= c\hat{a}^2c \\ &= c^2 \end{aligned}

Multiplying on both the left by \hat{b}\hat{a} and on the right by \hat{a}\hat{b} applies the rotation twice, and re-associating shows that this is equivalent to reflecting first in a and then in b^⊕This double-reflection formula for rotation is the form that works in any dimension; i.e. applies to vectors that may not lie completely in the plane of rotation.:

c_{\mathrm{rot} \times 2} = (\hat{b}\hat{a})c(\hat{a}\hat{b}) = \hat{b}(\hat{a}c\hat{a})\hat{b}

Applying the planarity condition twice to a product of four vectors shows that products of pairs of vectors in the same plane commute with one another:

\begin{aligned} (ab)(cd) &= (abc)d \\ &=(cba)d \\ &= c(bad) \\ &= c(dab) \\ &= (cd)(ab) \end{aligned}

For exactly the same reason, ratios of pairs of vectors in the plane also commute:

ab^{-1}cd^{-1} = cd^{-1}ab^{-1}

We have seen above that ratios of vectors in the plane behave similarly to complex numbers, so it’s comforting to see that they are commutative.

Coordinates

To better understand how the directed unit plane segment (unit bivector), I, behaves under the geometric product, it is useful to introduce a pair of orthogonal (perpendicular) unit vectors, e_1 and e_2, which can serve as coordinate basis vectors. Then I = e_1 e_2 = e_1 \wedge e_2.

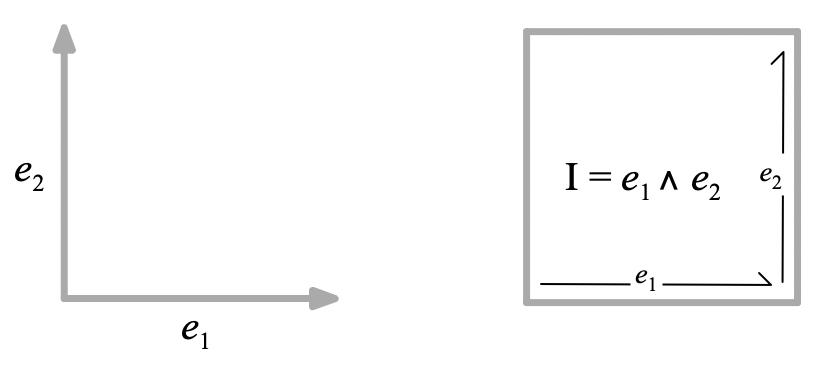
The condition that these are unit vectors is that they square to 1:

e_1^2 = e_2^2 = 1

and the condition that they are orthogonal is that they anti-commute, so that their geometric product is equal to their wedge product:

e_1 e_2 = - e_2 e_1 = e_1 \wedge e_2 = I

Since I can be written as a product of unit vectors, we expect that multiplying vectors in the plane by I will rotate them. Let’s consider what happens when we multiply the coordinate vectors on the right by I:

\begin{aligned} e_1 I &= e_1 e_1 e_2 = e_2 \\ e_2 I &= e_2 e_1 e_2 = - e_1 e_2 e_2 = - e_1 \end{aligned}

so right multiplication by I rotates both unit vectors counter-clockwise by 90 degrees. Any other vector in the plane can be written as a linear combination of these unit vectors, so right multiplication by I rotates any vector in the plane by 90 degrees counter-clockwise.

As expected for a right-angle rotation, I^2 = -1:

\begin{aligned} I^2 &= e_1 e_2 e_1 e_2 \\ &= e_1 (-e_1 e_2) e_2 \\ &= -e_1^2 e_2^2 \\ &= -1 \end{aligned}

which suggests why I behaved so similarly to the imaginary unit in some earlier formulas^⊕The fact that I squares to negative one lets us make sense of expressions like \exp(I \theta) = \cos(\theta) + I\sin(\theta) Just as for complex numbers, the strategy is to expand the exponential as a power series, reduce all higher powers of I using I^2 = -1 and then recognize the series for \sin and \cos..

Furthermore, we can show that I anti-commutes with any vector in the plane using the planarity condition to reverse products of three vectors in the plane, and anti-commutativity of orthogonal vectors to reverse e_1 and e_2

\begin{aligned} a I &= a e_1 e_2 \\ &= e_2 e_1 a \\ &= - e_1 e_2 a \\ &= - I a \end{aligned}

Since I is a product of a pair of vectors in the plane, it commutes with other products of pairs of vectors in the plane.

Duality

With this, we finally have enough preparation to understand the relationship between the parallelogram representations of the dot product and wedge product.

We set out to understand why

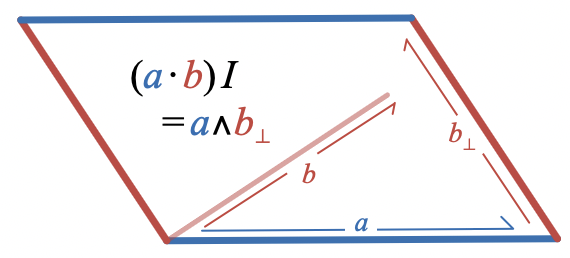
Duality of dot product and wedge product

(a \cdot b) I = a \wedge b_\perp

and we can now prove this result algebraically:

\begin{aligned} (a \cdot b) I &= \frac12 (ab + ba) I \\ &= \frac12 (abI + ba I) \\ &= \frac12 (abI - bIa) \\ &= \frac12 (a (bI) - (bI) a) \\ &= a \wedge (bI) \\ &= a \wedge b_\perp \end{aligned}

Let’s go through this calculation line by line:

Expand the dot product as the symmetric part of the geometric product
Distributivity of the geometric product
I anti-commutes with vectors in the plane, so it anti-commutes with a
The geometric product is associative
Recognize the anti-symmetric part of the geometric product as the wedge product
Right-multiplication of b by I rotates b counter-clockwise by 90 degrees, so we can identify bI with b_\perp

In the fifth step,

(a \cdot b) I = a \wedge (bI)

the unit bivector I acts in two interestingly different ways: on the left hand side, it is scaled by a \cdot b to make a bivector with the right magnitude; on the right hand side, it rotates b counter-clockwise by 90 degrees to produce a parallelogram spanned by vectors with the right direction relationship.

This relationship between the dot product and the wedge product is called “duality” because it gives a way of exchanging one kind of product for the other.

Scaling constrains what is easily visualized

The reason that this duality relationship is useful for visualizing the dot product is that the dot product depends linearly on two vectors, and if we draw the vectors as arrows on the page, then their dot product naturally has units of area on the page. Duality gives us a natural way to convert the scalar result of the dot product to a bivector, so that the grade matches the units.

This turns out to be a generally useful constraint: if you want to visualize some object built out of vectors on the page, its grade should match its units^⊕Most introductory-level discussions of geometry don’t really have the language to discuss grade, and frequently choose not to emphasize units either, so there is a fair amount of confusion about these points. In physics, it’s basically impossible to draw a “to scale” representation of the cross product of two vectors represented as arrows, because the cross product produces a vector (grade 1) with units of area.. This is why the dot product a \cdot b is very often visualized through one of the related projections (a \cdot \hat{b}) \hat{b} or (b \cdot \hat{a}) \hat{a}. The dot product alone is not easily visualizable because it is a scalar (grade 0), but it has units of area. The projections are visualizable because they are vectors (grade 1) with units of length.

The geometric product of two vectors contains a scalar (grade 0) and a bivector (grade 2), so if we want to visualize it, we need it to be unitless. This is why it’s easier to visualize the geometric ratio of two vectors (which is unitless) than the geometric product of two vectors (which has units of area).

Conclusion

The geometric product is an important unifying concept for representing Euclidean geometry algebraically. It combines the more familiar dot and wedge products into a single associative and invertible product, and clarifies their relationship. The geometric product represents rotations, reflections, and dilations through simple products or ratios of vectors, allows composing these operations with multiplication, and often allows simplifying these compositions by re-associating within the products. In this post, we were able to use this same trick over and over again to show that

The exterior angle rotations of a triangle compose to a full turn
The interior angles of a triangle compose to a half turn
Rotations and reflections preserve the length of vectors
The composition of two reflections is a rotation

and the geometric product makes it possible to reduce many more geometric proofs to algebra without ever needing to introduce coordinates or parameterizations of angles and trigonometric functions.

Thanks as usual to Jaime George for editing this post.

Shape Operator